![[KMP] Shortest Palindrome - ㄹㅇ 어려움 주의 🥲](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fpr72Z%2FbtsJG4kxcHH%2F0775ePw0s3A56rV5fKC6T1%2Fimg.png)


✨ 인사이트
Brute-force를 사용해서 (왼쪽부터 시작하는) 가장 긴 palindrome을 찾을 수 있다. 하지만 그것은 Time Complexity가 O(n^2)이다. 이보다 빠른 방법이 있다.
바로 KMP 알고리즘을 사용하는 것이다!
✨ 인사이트 - KMP 알고리즘
KMP 알고리즘은 특정 패턴이 주어진 텍스트 안에서 어디에 위치하는지 빠르게 찾는 방법이다.
이는 두 단계로 나뉜다.
1️⃣ LPS 배열 만들기
2️⃣ 이 배열을 활용해서 텍스트에서 패턴 찾기
LPS는 Longest Prefix which is also Suffix의 줄임말로, 0번째부터 k번째까지 (0 <= k <= len(s)-1) 자른 문자열의 앞에서부터 자른 문자열(prefix)들의 묶음과 뒤에서부터 자른 문자열(suffix)들의 묶음 중에서 가장 길게 겹치는 문자열의 길이를 입력한 배열이다.
말로 하면 어려우니 예시를 보자면,,
패턴 ABABC를 보자.
최초의 LPS 배열은 [0, 0, 0, 0, 0]이다.
편의상 LPS[0] = 0이다.
1번째까지 자른 문자열은 AB다.
prefix: A
suffix: B
겹치는 것은 없으므로 LPS[1] = 0이다.
2번째까지 자른 문자열은 ABA다. (ABA 전체를 자른 문자열이 아니라 "부분" 문자열임에 주의. 앞으로도 쭉 똑같다.)
prefix: A, AB
suffix: A, BA
겹치는 것 중 가장 긴 문자열은 A이므로 LPS[2] = 1이다.
3번째까지 자른 문자열은 ABAB다.
prefix: A, AB, ABA
suffix: B, AB, BAB
겹치는 것 중 가장 긴 문자열은 AB이므로 LPS[3] = 2이다.
4번째까지 자른 문자열은 ABABC다.
prefix: A, AB, ABA, ABAB
suffix: B, AB, BAB, BABC
겹치는 것은 없으므로 LPS[4] = 1이다.
따라서 LPS는 [0, 0, 1, 2, 0]이 된다.
이제 이 LPS를 가지고 텍스트에서 패턴을 찾아내자!
(우리가 풀 문제에서는 LPS 배열만 완성하는 것으로 충분하지만,, 그래도 KMP 알고리즘을 끝까지 알면 좋잖슴!!)

(원래 주저리주저리 썼는데 가독성이 안 좋아서 chatGPT 캡처로 대체함 ㅜㅜ)



👟 알고리즘 설명
1. 주어진 배열 s에 대해 s + "#" + s[::-1]을 만든다. (#은 둘을 구분하기 위해 끼웠다.)
2. 새롭게 만든 문자열에 대해 Prefix Table을 만든다.
def _build_prefix_table(s): #앞에 있는 언더스코어(_)는 이 함수는 클래스 내부에서만 쓰이기를 희망한다는 뜻
prefix_table = [0] * len(s) # Prefix Table을 s의 길이만큼 초기화
length = 0 # 일치하는 접두사와 접미사의 길이를 저장하는 변수
for i in range(1, len(s)): # 두 번째 문자부터 시작 (i = 1부터)
while length > 0 and s[i] != s[length]: # 불일치가 발생하면
length = prefix_table[length - 1] # 이전 접두사로 되돌아감
if s[i] == s[length]: # 일치하면
length += 1 # 접두사-접미사 길이를 증가
prefix_table[i] = length # Prefix Table에 길이를 저장
return prefix_table
# 접두사: prefix, 접미사: suffix
아래 예시를 하나씩 따라가며 이 과정이 어떻게 발생하나 보자.

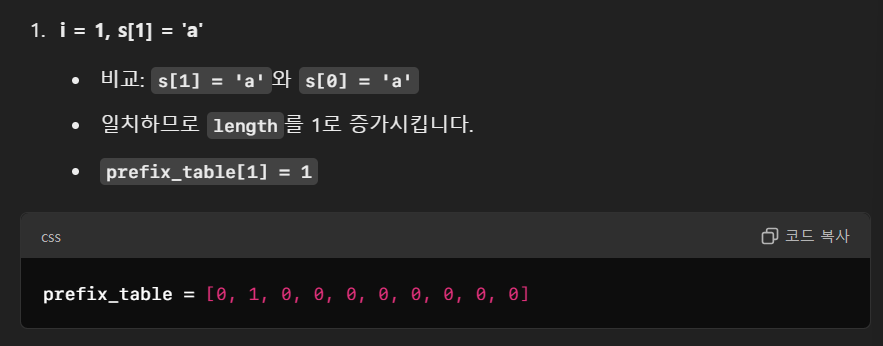
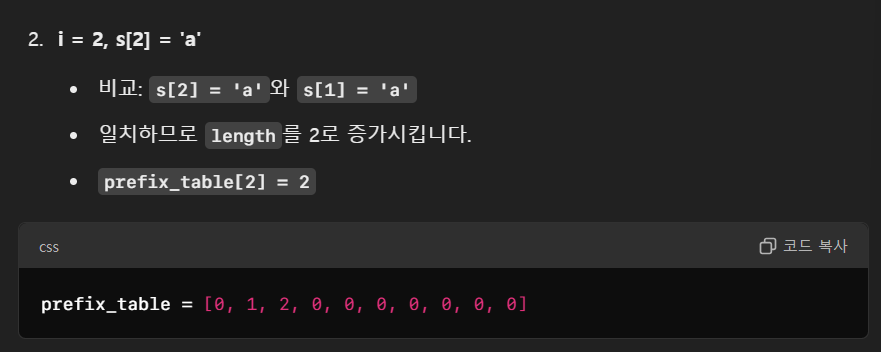
그런데 여기서 주목해야 한다.
(아래 사진에 왜 숫자가 다시 1부터 시작하냐면 빌어먹을 chatGPT가 헛소리해서 고치느라 새로 만들어서 그렇다 ㅎ)

aaab에서 aaa와 aab를 비교했는데 이들이 같지가 않다. 그렇다면 한 단계 양보해야 한다. 이를 length는 2에서 1로 줄어든다.
그렇다면 이제는 aa와 ab를 비교해야 하는데 이 역시 같지가 않다. 다시 한 단계 양보한다. 그러면 length는 1에서 0으로 줄어들고 while문 조건에 맞지 않아 탈출하게 된다.
i=4부터 다시 진행된다.
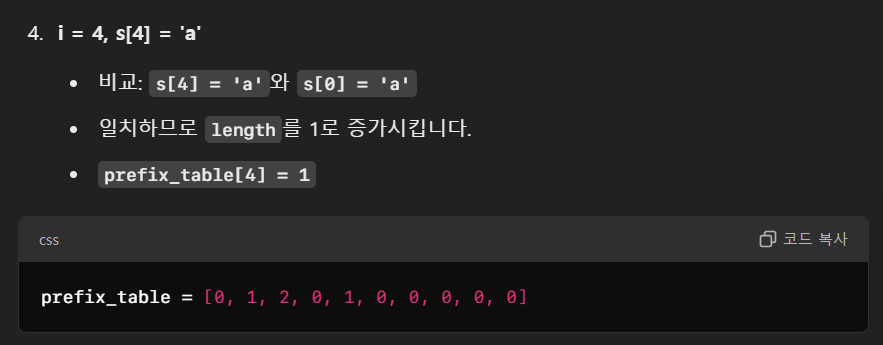

그리고 다시 불일치가 발생한다.

이후 그냥 무난하게 흘러가서 최종적으로 다음과 같이 prefix_table이 나온다.
prefix_table = [0, 1, 2, 0, 1, 2, 0, 1, 2, 3]
3. combined string에 prefix table을 만들고 답을 구한다.
def shortestPalindrome(self, s: str) -> str:
# Reverse the original string
reversed_string = s[::-1]
# Combine the original and reversed strings with a separator
combined_string = s + "#" + reversed_string
# Build the prefix table for the combined string
prefix_table = self._build_prefix_table(combined_string)
# Get the length of the longest palindromic prefix
palindrome_length = prefix_table[-1]
# Construct the shortest palindrome by appending the reverse of the suffix
suffix = reversed_string[: len(s) - palindrome_length]
return suffix + s
prefix_table[-1]은 곧, 왼쪽에서부터 시작하여 가장 긴 palindrome의 길이를 나타낸다.
다시 방법을 정리하면,
1️⃣ 문자열 s를 가운데에 #이라는 delimiter를 두고 오른쪽에 거꾸로 붙인다
2️⃣ prefix table을 만든다(이것은 KMP 알고리즘의 한 단계인 "LPS 배열"을 만드는 것이다.)
3️⃣ prefix table[-1]이 가장 긴 palindrome이기 때문에 이를 통해 답을 구한다.
✅ 정답
Time Complexity: O(n)
Space Complexity: O(n)
class Solution:
def shortestPalindrome(self, s: str) -> str:
# Reverse the original string
reversed_string = s[::-1]
# Combine the original and reversed strings with a separator
combined_string = s + "#" + reversed_string
# Build the prefix table for the combined string
prefix_table = self._build_prefix_table(combined_string)
# Get the length of the longest palindromic prefix
palindrome_length = prefix_table[-1]
# Construct the shortest palindrome by appending the reverse of the suffix
suffix = reversed_string[: len(s) - palindrome_length]
return suffix + s
# Helper function to build the KMP prefix table
def _build_prefix_table(self, s: str) -> list:
prefix_table = [0] * len(s)
length = 0
# Build the table by comparing characters
for i in range(1, len(s)):
while length > 0 and s[i] != s[length]:
length = prefix_table[length - 1]
if s[i] == s[length]:
length += 1
prefix_table[i] = length
return prefix_table
그나저나, prefix table의 time complexity가 O(n)인 이유가 이해가 되지 않았다.
왜냐면 for 안에 while이 있는데 while은 하나씩 훑기 때문에 사실상 while 역시 n번 반복될 수 있기 때문이다.
하지만,, 그렇지 않다.
이런저런 설명들을 찾아보고 chatGPT한테도 물어봤는데 내가 생각하기에 가장 쉬운 생각법은 이것이다.
아래 사항들을 하나씩 음미해 보자.
- length가 (순순히) 1이 늘어난다는 것은 while문을 거치지 않았다는 뜻이다.
- length가 while문을 여러 번 반복할 수 있다. 하지만 그 최대 횟수는 현재의 length만큼 뿐이다.
whlie문은 기존의 length를 허무는 것밖에 하지 못한다.
그러니까 i가 1부터 점점 커갈 때, 예를 들어 1부터 k까지 열심히 쌓았는데 k+1에서 신나게 while문이 돌면서 length를 0까지 만든 k번의 추가적인 연산을 요구한다. 이 연산의 수는 1번부터 k번까지 고르게 1번씩 나눠줄 수 있기 때문에 i가 k+1까지 늘어나는 동안의 연산의 수는 최대 2k인 것이다!
즉, 이를 n까지 확대하면 O(n)이 time complexity가 된다.
'분명 전산학부 졸업 했는데 코딩 개못하는 조준호 > 알고리즘 초고수 조준호' 카테고리의 다른 글
| [Rolling Hash] Shortest Palindrome (0) | 2024.09.24 |
|---|---|
| [Matrix] Spiral Matrix IV (0) | 2024.09.09 |
| [Hash Table, Linked List] Delete Nodes From Linked List Present in Array (1) | 2024.09.06 |
| [Array] Find the Student that Will Replace the Chalk (0) | 2024.09.03 |
| [Binary Search, Two Pointers] Find K-th Smallest Pair Distance (0) | 2024.08.17 |

한국은행 들어갈 때까지만 합니다
조만간 티비에서 봅시다
![[Rolling Hash] Shortest Palindrome](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FRynJf%2FbtsJJKmC9Az%2F1Vdp2L2d6KR6gVhwkR0tUk%2Fimg.png)
![[Matrix] Spiral Matrix IV](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F7DCFO%2FbtsJw2TFdul%2Frhjgl9xA8yQ6uF1Tq0mGWK%2Fimg.png)
![[Hash Table, Linked List] Delete Nodes From Linked List Present in Array](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F8DpD5%2FbtsJux7V2HT%2FI2ZDVQN9bXnOg1k3fRom2k%2Fimg.png)
![[Array] Find the Student that Will Replace the Chalk](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FMYROI%2FbtsJqd9aaZd%2Ffn0MZW8wAcxtb8QtWOo2F1%2Fimg.png)