![[DP] Filling Bookcase Shelves](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FuX6Uk%2FbtsI6ZcyI6s%2FPq7Tm9ZANvHNklskMHgKh1%2Fimg.png)

leetcode/240731_Filling Bookcase Shelves/explanation.md at main · Yellome-in-the-BOK/leetcode
Contribute to Yellome-in-the-BOK/leetcode development by creating an account on GitHub.
github.com



✨ 인사이트
보자마자 당연히 Dynamic Programming을 써야 할 것 같았다. 맞긴 한데 그냥 감일뿐이었고,, 어떤 경우에 DP를 써야 하는지 이번 기회에 알아보기로 했다.
🍯 꿀팁 - 어떤 경우에 DP를 써야 하는가?
1. 최적 부분 구조 (Optimal Substructure)
문제를 작은 부분 문제로 나눌 수 있고, 이 부분 문제들의 optimum을 통해 전체 문제의 optimum을 구할 수 있을 때
ex. 최단 경로 문제
2. 중복되는 부분 문제 (Overlapping Subproblems)
부분 문제가 여러 번 재사용될 때
ex. 피보나치 수열
3. 상태와 상태 전이 (State and State Transition)
현재 상태와 이전 상태 간의 관계를 정의할 수 있을 때
🍯 꿀팁 - DP의 대표적 방법
메모이제이션 (Memoization)
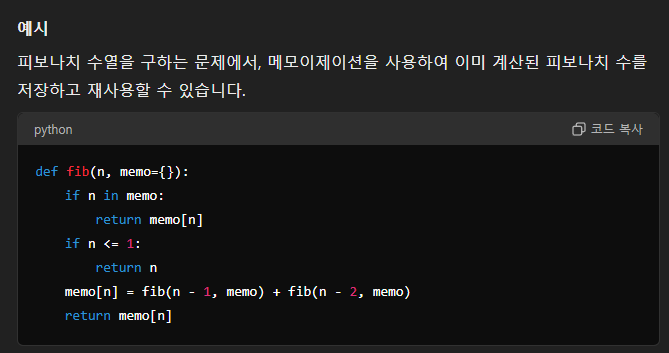
Top-Down (최상위에서 시작하여 점차적으로 하위 문제 해결)
주로 재귀 함수 사용
장점: 필요한 부분만 계산해서 효율적
단점: 재귀 호출로 stack overflow의 위험
테이블 방식 (Tabulation)

Bottom-Up (작은 문제부터 시작해서 점차적으로 큰 문제 해결)
주로 반복문 사용
장점: 순서대로 해결하므로 stack overflow 위험이 없음
단점: 모든 부분 문제를 계산하기 때문에 비효율적
🫠 망한 내 풀이 (사유: TLE)
Time Complexity: O(2^n)
Space Complexity: O(n)
# 100% 혼자
class Solution:
def minHeightShelves(self, books: List[List[int]], shelf_width: int) -> int:
dp_list = [float("inf") for _ in range(len(books)+1)]
dp_list[0] = 0
def dp(book_num: int, remain_width: int, prev_shelf_book_num: int, this_shelf_height: int) -> int:
if book_num == len(books)+1: return
book_width, book_height = books[book_num-1][0], books[book_num-1][1]
dp_list[book_num] = min(dp_list[book_num], dp_list[book_num-1]+book_height)
dp(book_num+1, shelf_width-book_width, book_num-1, book_height)
if remain_width != shelf_width and book_width <= remain_width:
dp_list[book_num] = min(dp_list[book_num], dp_list[prev_shelf_book_num]+max(this_shelf_height, book_height))
dp(book_num+1, remain_width-book_width, prev_shelf_book_num, max(this_shelf_height, book_height))
dp(1, shelf_width, 0, books[0][1])
return dp_list[len(books)]
dp 안에 dp를 두 개나 넣어버린 기가 막힌 능지처참으로 매번 2개의 선택지가 새로 생겼고 exponential이라는 전무후무한 time complexity가 나와서 방금 벌로 1시간 동안 에어컨 껐음.

✅ 정답
Time Complexity: O(n^2)
Space Complexity: O(n)
class Solution:
def minHeightShelves(self, books: List[List[int]], shelf_width: int) -> int:
n = len(books)
# dp[i]는 i번째 책까지 놓았을 때 최소 높이
dp = [float("inf")] * (n + 1)
dp[0] = 0
for i in range(1, n + 1):
width = 0 # 현재 선반 총 너비
height = 0 # 현재 선반 최대 높이
for j in range(i, 0, -1):
width += books[j - 1][0]
if width > shelf_width:
break
height = max(height, books[j - 1][1])
dp[i] = min(dp[i], dp[j - 1] + height)
return dp[n]
첫 번째 루프에서 i번째 책을 '마지막으로' 배치하는 경우를 고려한다.
두 번째 루프에서는 i번째부터 i-1, i-2, i-3... 이런 식으로 뒤로 거슬러 가며 책의 두께를 모두 더해 width에 저장한다. (이 값이 shelf_width보다 크지 않을 때까지만)
i부터 j(<=i)까지 한 선반 위에 놓을 수 있다고 하면 일단 현재 선반의 최대 높이 height를 다시 정해주고, dp[i]의 값도 다시 정해준다.
height 계산은 직관적이니까 넘어가고,
dp[i]의 경우를 보면, dp[j-1]는 j보다 더 전, 그러니까 이전 선반까지의 높이를 모두 더한 다음에 현재 선반의 높이 height를 정하는 식으로 계산한다.
루프가 O(n^2)만큼 돌며 그 안에 있는 dp[i]나 dp[j-1]의 경우도 이미 있는 값이기 때문에 추가적으로 드는 시간은 없다.
따라서 Time Complexity: O(n^2), Space Complexity: O(n)로 가볍게 결정된다.
'분명 전산학부 졸업 했는데 코딩 개못하는 조준호 > 알고리즘 초고수 조준호' 카테고리의 다른 글
| [Backtracking] Combination Sum II (0) | 2024.08.17 |
|---|---|
| [BFS, DFS] Regions Cut By Slashes (0) | 2024.08.17 |
| [DP] Minimum Deletions to Make String Balanced (0) | 2024.08.17 |
| [DP] Count Number of Teams (0) | 2024.08.17 |
| [Array, Greedy, Sorting] Minimum Difference Between Largest and Smallest Value in Three Moves (1) | 2024.07.03 |

한국은행 들어갈 때까지만 합니다
조만간 티비에서 봅시다
![[Backtracking] Combination Sum II](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fc5yrfI%2FbtsI6dbvT4y%2FyVZbvoss6oaEPWQqI2D3cK%2Fimg.png)
![[BFS, DFS] Regions Cut By Slashes](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcFqh7x%2FbtsI7IBhEFh%2FwFLgNX8fQzRV8HCoMnd60k%2Fimg.png)
![[DP] Minimum Deletions to Make String Balanced](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FUjv99%2FbtsI6CB83D1%2FdyusTjnDKzQBklVGmrhM80%2Fimg.png)
![[DP] Count Number of Teams](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fv7b63%2FbtsI7W0nuDg%2Fm4xhk4XP4IvoVDTomEdreK%2Fimg.png)