

improved parameters로 만든 모델을 해부해 보자.
model.summary()
이렇게 입력을 하면 아주 길게 이것저것 나오니까 잘라서 확인하자.
Model: "gradient_boosted_trees_model_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
=================================================================
Total params: 1
Trainable params: 0
Non-trainable params: 1
_________________________________________________________________
먼저 모델의 개요가 나온다. 모델의 이름, 총 파라미터 수, 레이어에 대한 정보가 나온다.
GBT 모델은 특별한 레이어가 없기 때문에 레이어 관련 정보는 생략되어 있다.
Neural Network는 대부분 레이어로 구성되는데 예시를 들면 다음과 같다.

이 경우 개요를 보면 다음처럼 나온다.

Neural Network 모델의 경우 훈련 가능한 파라미터는 weight와 bias다. 이는 Back-propagation 알고리즘을 통해 학습된다. 하지만 GBT에는 weight와 bias가 없으며, 훈련 가능한 파라미터가 없다. Decision Trees들로 구성되어 있기 때문에 Neural Network 모델과는 방식이 다르다.
GBT는 트리의 구조를 학습한다.

weight와 bias는 연속적인 반면 트리의 구조는 연속적이지 않아서 non-trainable parameter라고 부른다.
GBT 모델에서 전체 parameter의 수는 1로 표시되는데 이는 그냥 모델의 구조적 메타 데이터를 나타내는 것뿐이며 숫자 자체는 크게 의미가 없다.
Type: "GRADIENT_BOOSTED_TREES"
Task: CLASSIFICATION
Label: "__LABEL"
다음으로 모델의 유형과 태스크가 나온다.
유형은 알다시피 GBT다. 태스크는 classification이다. 생존 여부를 예측해야 하니 분류다.
Label은 모델이 예측하려는 타깃 변수다. "Survived"로 설정돼야 하는데 왜 이렇게 들어갔나 모르겠다.
다음은 Input Features다.
Input Features (11):
Age
Cabin
Embarked
Fare
Name
Parch
Pclass
Sex
SibSp
Ticket_item
Ticket_number
다음으로는 변수 중요도(Variable Importance)가 여러 개 나온다.
이는 모델이 학습하는 과정에서 각 feature를 얼마나 중요하게 사용했는지를 나타내는 지표다.
(첫 줄의 No weights는 GBT가 weight를 계산하지 않기 때문에 있음)
No weights
Variable Importance: INV_MEAN_MIN_DEPTH:
1. "Sex" 0.576632 ################
2. "Age" 0.364297 #######
3. "Fare" 0.278839 ####
4. "Name" 0.208548 #
5. "Ticket_number" 0.180792
6. "Pclass" 0.176962
7. "Parch" 0.176659
8. "Ticket_item" 0.175540
9. "Embarked" 0.172339
10. "SibSp" 0.170442
INV_MEAN_MIN_DEPTH는 각 feature들이 트리의 평균 최소 깊이에서 얼마나 자주 사용되었는지를 나타낸다. 평균 최소 깊이는 해당 Feature가 처음으로 사용된 깊이의 평균을 의미한다. 그러니까 Decision Tree가 갈라질 때 root에서 가까운 곳에서 해당 feature가 사용될수록 중요하다는 것을 직관적으로 알 수 있다.
깊이의 역수로 만들었기 때문에 값이 클수록 중요함!
Variable Importance: NUM_AS_ROOT:
1. "Sex" 28.000000 ################
2. "Name" 5.000000
Variable Importance: NUM_NODES:
1. "Age" 406.000000 ################
2. "Fare" 290.000000 ###########
3. "Name" 44.000000 #
4. "Ticket_item" 42.000000 #
5. "Sex" 31.000000 #
6. "Parch" 28.000000
7. "Ticket_number" 22.000000
8. "Pclass" 15.000000
9. "Embarked" 12.000000
10. "SibSp" 5.000000
Variable Importance: SUM_SCORE:
1. "Sex" 460.497828 ################
2. "Age" 355.963333 ############
3. "Fare" 292.870316 ##########
4. "Name" 108.548952 ###
5. "Pclass" 28.132254
6. "Ticket_item" 23.818676
7. "Ticket_number" 23.772288
8. "Parch" 19.303155
9. "Embarked" 8.155722
10. "SibSp" 0.015225
차례로, 각 feature가 root node로 얼마나 많이 사용됐나, 각 feature가 트리의 node에서 얼마나 많이 사용됐나, 각 feature가 기여한 총점수를 나타낸다.
다음으로 모델의 성능을 평가한 부분이다.
Loss: BINOMIAL_LOG_LIKELIHOOD
Validation loss value: 1.01542
이 모델은 손실 함수로 binomial log likelihood를 사용하고 있다. 이는 이진 분류나 GBT에서 자주 사용된다.
loss는 1.01 정도다. 물론 작을수록 좋다.
Number of trees per iteration: 1
Node format: NOT_SET
Number of trees: 33
Total number of nodes: 1823
다음은 트리 구성 정보에 대한 내용이다.
첫 번째 줄은, 각 iteration마다 트리가 하나 추가된다는 뜻이다. 한 번에 여러 트리를 추가할 수 있는데, 이러면 속도는 빨라지지만 정확도는 작아진다.
두 번째 줄은, 노드 형식을 설정하지 않았음을 나타낸다. 일반적으로 기본값을 사용한다.
세 번째 줄은, 모델에 포함된 트리의 총 개수,
네 번째 줄은, 모델에 포함된 노드의 총개수를 나타낸다.
Number of nodes by tree:
Count: 33 Average: 55.2424 StdDev: 5.13473
Min: 39 Max: 63 Ignored: 0
----------------------------------------------
다음은 구체적으로 트리별 노드 수 분포를 나타낸다.
아래처럼 시각화해서도 보여준다.
[ 39, 40) 1 3.03% 3.03% #
[ 40, 41) 0 0.00% 3.03%
[ 41, 42) 0 0.00% 3.03%
[ 42, 44) 0 0.00% 3.03%
[ 44, 45) 0 0.00% 3.03%
[ 45, 46) 0 0.00% 3.03%
[ 46, 47) 0 0.00% 3.03%
[ 47, 49) 2 6.06% 9.09% ###
[ 49, 50) 2 6.06% 15.15% ###
[ 50, 51) 0 0.00% 15.15%
[ 51, 52) 2 6.06% 21.21% ###
[ 52, 54) 5 15.15% 36.36% #######
[ 54, 55) 0 0.00% 36.36%
[ 55, 56) 5 15.15% 51.52% #######
[ 56, 57) 0 0.00% 51.52%
[ 57, 59) 4 12.12% 63.64% ######
[ 59, 60) 7 21.21% 84.85% ##########
[ 60, 61) 0 0.00% 84.85%
[ 61, 62) 3 9.09% 93.94% ####
[ 62, 63] 2 6.06% 100.00% ###
leaf node에 대해서도 알려준다.
Depth by leafs:
Count: 928 Average: 4.8847 StdDev: 0.380934
Min: 2 Max: 5 Ignored: 0
----------------------------------------------
이거는 leaf node의 깊이 분포다. 대부분 깊이가 5다.
[ 2, 3) 1 0.11% 0.11%
[ 3, 4) 17 1.83% 1.94%
[ 4, 5) 70 7.54% 9.48% #
[ 5, 5] 840 90.52% 100.00% ##########
아래는 leaf node의 훈련 관측치 수를 나타낸다.
Number of training obs by leaf:
Count: 928 Average: 28.4127 StdDev: 70.8313
Min: 1 Max: 438 Ignored: 0
----------------------------------------------
훈련 관측치 수(Number of Training Observations)는 학습 과정에서 각 노드로(특히 leaf node)로 분할된 데이터 포인트(관측치)의 개수를 나타낸다.
Decision Tree 모델에서 leaf node는 최종 예측 값(이 때문에 internal node나 leaf node나 분류하기는 하지만 최종 값을 나타내는 leaf node에 더 주목해야 한다.)을 나타내기 때문에 각 leaf node에 할당된 데이터 포인트의 수가 높을수록 예측 정확도가 높다.
[ 1, 22) 731 78.77% 78.77% ##########
[ 22, 44) 74 7.97% 86.75% #
[ 44, 66) 37 3.99% 90.73% #
[ 66, 88) 3 0.32% 91.06%
[ 88, 110) 9 0.97% 92.03%
[ 110, 132) 8 0.86% 92.89%
[ 132, 154) 18 1.94% 94.83%
[ 154, 176) 8 0.86% 95.69%
[ 176, 198) 6 0.65% 96.34%
[ 198, 220) 2 0.22% 96.55%
[ 220, 241) 2 0.22% 96.77%
[ 241, 263) 1 0.11% 96.88%
[ 263, 285) 2 0.22% 97.09%
[ 285, 307) 5 0.54% 97.63%
[ 307, 329) 1 0.11% 97.74%
[ 329, 351) 2 0.22% 97.95%
[ 351, 373) 6 0.65% 98.60%
[ 373, 395) 6 0.65% 99.25%
[ 395, 417) 2 0.22% 99.46%
[ 417, 438] 5 0.54% 100.00%
편차가 매우 크다.
이 아래는 features에 대한 설명이다.
Attribute in nodes:
406 : Age [NUMERICAL]
290 : Fare [NUMERICAL]
44 : Name [CATEGORICAL_SET]
42 : Ticket_item [CATEGORICAL]
31 : Sex [CATEGORICAL]
28 : Parch [NUMERICAL]
22 : Ticket_number [CATEGORICAL]
15 : Pclass [NUMERICAL]
12 : Embarked [CATEGORICAL]
5 : SibSp [NUMERICAL]
각 node에서 사용된 feature의 전체 횟수를 나타내고 있다.
그리고 이 아래는 횟수를 깊이별로 쪼개놓았다.
Attribute in nodes with depth <= 0:
28 : Sex [CATEGORICAL]
5 : Name [CATEGORICAL_SET]
Attribute in nodes with depth <= 1:
39 : Age [NUMERICAL]
28 : Sex [CATEGORICAL]
21 : Fare [NUMERICAL]
5 : Name [CATEGORICAL_SET]
3 : Pclass [NUMERICAL]
2 : Ticket_number [CATEGORICAL]
1 : Parch [NUMERICAL]
Attribute in nodes with depth <= 2:
102 : Age [NUMERICAL]
65 : Fare [NUMERICAL]
28 : Sex [CATEGORICAL]
15 : Name [CATEGORICAL_SET]
7 : Ticket_number [CATEGORICAL]
5 : Pclass [NUMERICAL]
4 : Parch [NUMERICAL]
2 : Ticket_item [CATEGORICAL]
2 : Embarked [CATEGORICAL]
Attribute in nodes with depth <= 3:
206 : Age [NUMERICAL]
156 : Fare [NUMERICAL]
33 : Name [CATEGORICAL_SET]
29 : Sex [CATEGORICAL]
19 : Ticket_number [CATEGORICAL]
11 : Ticket_item [CATEGORICAL]
11 : Parch [NUMERICAL]
7 : Pclass [NUMERICAL]
3 : Embarked [CATEGORICAL]
Attribute in nodes with depth <= 5:
406 : Age [NUMERICAL]
290 : Fare [NUMERICAL]
44 : Name [CATEGORICAL_SET]
42 : Ticket_item [CATEGORICAL]
31 : Sex [CATEGORICAL]
28 : Parch [NUMERICAL]
22 : Ticket_number [CATEGORICAL]
15 : Pclass [NUMERICAL]
12 : Embarked [CATEGORICAL]
5 : SibSp [NUMERICAL]
depth가 작은 쪽에서 많이 쓰일수록 중요한 feature다.
다음은 각 노드에서 분할 기준으로 어떤 것이 사용되었나를 보여준다.
Condition type in nodes:
744 : ObliqueCondition
122 : ContainsBitmapCondition
29 : ContainsCondition
이건 깊이별로 보여준다.
Condition type in nodes with depth <= 0:
31 : ContainsBitmapCondition
2 : ContainsCondition
Condition type in nodes with depth <= 1:
64 : ObliqueCondition
33 : ContainsBitmapCondition
2 : ContainsCondition
Condition type in nodes with depth <= 2:
176 : ObliqueCondition
51 : ContainsBitmapCondition
3 : ContainsCondition
Condition type in nodes with depth <= 3:
380 : ObliqueCondition
77 : ContainsBitmapCondition
18 : ContainsCondition
Condition type in nodes with depth <= 5:
744 : ObliqueCondition
122 : ContainsBitmapCondition
29 : ContainsCondition
이 역시 depth가 작은 쪽에서 많이 쓰일수록 중요한 분할 기준이다.
Training logs:
Number of iteration to final model: 33
Iter:1 train-loss:1.266350 valid-loss:1.360049 train-accuracy:0.624531 valid-accuracy:0.543478
Iter:2 train-loss:1.213702 valid-loss:1.321897 train-accuracy:0.624531 valid-accuracy:0.543478
Iter:3 train-loss:1.165783 valid-loss:1.286817 train-accuracy:0.624531 valid-accuracy:0.543478
Iter:4 train-loss:1.122469 valid-loss:1.256133 train-accuracy:0.624531 valid-accuracy:0.543478
Iter:5 train-loss:1.081461 valid-loss:1.229342 train-accuracy:0.808511 valid-accuracy:0.771739
Iter:6 train-loss:1.045305 valid-loss:1.204601 train-accuracy:0.826033 valid-accuracy:0.728261
Iter:16 train-loss:0.794952 valid-loss:1.058568 train-accuracy:0.914894 valid-accuracy:0.771739
Iter:26 train-loss:0.646146 valid-loss:1.021539 train-accuracy:0.926158 valid-accuracy:0.793478
Iter:36 train-loss:0.558627 valid-loss:1.023663 train-accuracy:0.929912 valid-accuracy:0.771739
Iter:46 train-loss:0.493899 valid-loss:1.025164 train-accuracy:0.931164 valid-accuracy:0.760870
Iter:56 train-loss:0.451528 valid-loss:1.032880 train-accuracy:0.938673 valid-accuracy:0.771739
이건 각 iteration마다 성능이 어떻게 변했나를 알려준다.
train-loss는 시간이 지나면서 점점 감소하고 있는데 이는 모델이 갈수록 train data에 더 적합해지고 있다는 것을 나타낸다. 하지만 valid-loss는 어느 수준에서 정체되는 것을 보이는데 이것은 모델의 실제 성능이 더 이상 좋아지지는 않는다는 것을 보여준다. 이는 accuracy에서도 확인할 수 있다.
그러니까 더 iteration을 해봤자 과적합만 일어나고 실제 성능 개선은 계속되지 않는다는 것이다.
모델을 만들고, 어떻게 생겼나 해부도 해봤으니 실제 예측을 수행할 차례다!
def prediction_to_kaggle_format(model, threshold=0.5):
proba_survive = model.predict(serving_ds, verbose=0)[:, 0]
return pd.DataFrame({
"PassengerId": serving_df["PassengerId"],
"Survived": (proba_survive >= threshold).astype(int)
})
parameter에 있는 model은 우리가 가져다 쓴 모델, threshold는 임곗값을 나타낸다.
임곗값이란 뭐냐면,
이진 분류 문제에서 예측 값은 0.5383821 이런 식으로 소수점으로 나올 텐데 이 값을 이분법으로 나눠야 하기 때문에 어떤 경계를 기준으로 나눌 것인지를 정하는 것이다.
mode.predict() 함수에 (test.csv를 변형한) serving_ds를 넣어주고 verbose는 0으로 설정해서 출력 메시지를 최소화한다.
끝에 붙은 [:, 0]는 각 데이터에 대해 생존 확률만 뽑아준다.
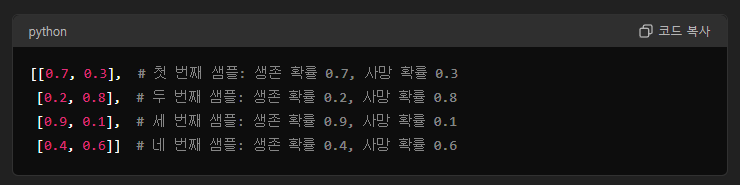
각 데이터에 대해 이런 식으로 나오는데 [:, 0]를 사용하면

이렇게 생존 확률들만 나온다.
마지막으로 return 부분만 다시 가져오면,
return pd.DataFrame({
"PassengerId": serving_df["PassengerId"],
"Survived": (proba_survive >= threshold).astype(int)
})
마지막 줄은 생존 확률이 threshold보다 큰 경우 True를 반환하고 이것을 astype(int)를 통해 True는 1로, False는 0으로 반환한다.
def make_submission(kaggle_predictions):
path="/kaggle/working/submission.csv"
kaggle_predictions.to_csv(path, index=False)
print(f"Submission exported to {path}")
이 함수는 예측 결과를 경로를 지정해서 CSV 파일로 저장한다.
kaggle_predictions = prediction_to_kaggle_format(model)
make_submission(kaggle_predictions)
!head /kaggle/working/submission.csv
이건 위에서 만든 두 함수를 사용한 것이고,
마지막 줄은 쉘 명령어인데 해당 CSV 파일 맨 위의 10줄을 출력한다.
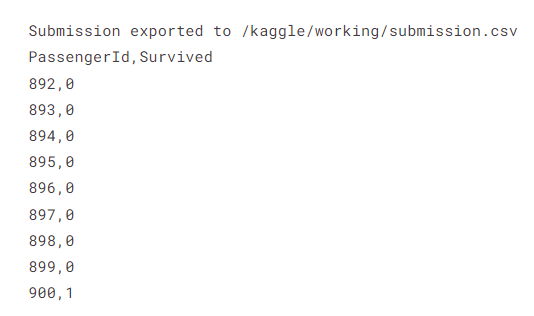
900번은 살고 892~899번은 죽었다고 예측한 모습.
'분명 전산학부 졸업 했는데 코딩 개못하는 조준호 > AI, ML, DL' 카테고리의 다른 글
| Kaggle Competition - Binary Prediction of Poisonous Mushrooms (1) EDA 전까지 (1) | 2024.09.02 |
|---|---|
| 역시 ML의 시작은 타이타닉 - (5) hyperparameter 튜닝 (8) | 2024.07.24 |
| 역시 ML의 시작은 타이타닉 - (3) 모델 만들고 학습시키고 평가하기 (7) | 2024.07.20 |
| 역시 ML의 시작은 타이타닉 - (2) Preprocess 후 Tensorflow DataSet으로 전환 (0) | 2024.07.20 |
| 역시 ML의 시작은 타이타닉 - (1) Dependencies 가져오기 (0) | 2024.07.20 |

한국은행 들어갈 때까지만 합니다
조만간 티비에서 봅시다



